#4 Metode Grafik Menyelesaikan Sistem Persamaan Linear Dua Variabel

Friday, November 01, 2019

Untuk menyelesaikan SPLDV menggunakan metode grafik, himpunan penyelesaian dari sistem persamaan linear dua variabel adalah koordinat titik potong dua garis (grafik) tersebut. Jadi anda harus mencari titik potong garis tersebut di koordinat y dengan membuat x = 0 yang akan berpotongan di (0, y), dan mencari titik potong garis tersebut di koordinat x dengan membuat y = 0 yang akan berpotongan di (x, 0). Kemudian menarik kedua garis tersebut sehingga berpotongan di suatu titik koordianat (x,y). Supaya lebih paham coba simaklah contoh soal di berikut.

Contoh Soal 1

Dengan metode grafik, tentukan himpunan penyelesaian sistem persamaan linear dua variabel x + y = 4 dan x + 3y = 6 jika x, y variabel pada himpunan bilangan real.

Penyelesaian:

Seperti yang sudah dijelaskan di atas, Anda harus mencari koordinat titik potong di x dan y pada persamaan x + y = 4 dan x + 3y = 6. Sekarang kita cari titik potong di x dan y persamaan x + y = 4, yakni:

jika x = 0, maka:

x + y = 4

0 + y = 4

       y = 4 
Maka titik potong di y (0, 4)

jika y = 0, maka:

x + y = 4

x + 0 = 4

       x = 4
Maka  titik potong di x (4, 0)

Jadi titik potong persamaan x + y = 4 adalah (0,4) dan (4,0)

Selanjutnya cari titik potong di x dan y persamaan x + 3y = 6, yakni:

jika x = 0, maka:

x + 3y = 6

0 + 3y = 6

       3y = 6 
         y = 6/2
         y = 3
Maka titik potong di y (0, 2)

jika y = 0, maka:

x + 2y = 6

x + 0 = 6

       x = 6
Maka titik potong di x (6, 0)

Jadi titik potong persamaan x + 2y = 6 adalah (0,2) dan (6,0)

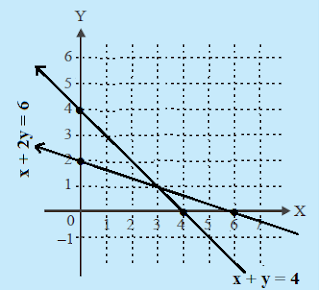
Sekarang buat garis dari kedua persamaan tersebut berdasarkan titik potong, yakni seperti gambar di bawah ini.

Berdasarkan gambar grafik sistem persamaan dari x + y = 4 dan x + 3y = 6 di atas tampak bahwa koordinat titik potong kedua garis adalah (3, 1). Jadi, himpunan penyelesaian dari sistem persamaan x + y = 4 dan x + 3y = 6 adalah {(3, 1)}.

Nah penjelasan di atas merupakan penyelesaian sistem persamaan linear dua variabel jika kedua garis itu berpotongan di suatu titik koordinat. Bagaimana kalau kedua garis tersebut tidak pernah berpotongan?

Jika garis-garisnya tidak berpotongan di satu titik tertentu maka himpunan penyelesaiannya adalah himpunan  kosong. Berikut contoh soal sistem persamaan linear dua variabel yang menghasilkan penyelesaian berupa himpunan kosong.

Contoh Soal 2

Dengan metode grafik, tentukan himpunan penyelesaian sistem persamaan

linear dua variabel x + 2y = 2 dan 2x + 4y = 8 jika x, y variabel pada himpunan bilangan real.

Penyelesaian:

Sekarang kita cari titik potong di x dan y persamaan x + 2y = 2, yakni:

jika x = 0, maka:

x + 2y = 2

0 + y = 1

       y = 1 
Maka titik potong di y (0, 1)

jika y = 0, maka:

x + 2y = 2

x + 0 = 2

       x = 2
Maka titik potong di x (2, 0)

Jadi titik potong persamaan x + 2y = 2 adalah (0,1) dan (2,0)

Selanjutnya kita cari titik potong di x dan y persamaan 2x + 4y = 8, yakni:

jika x = 0, maka:

2x + 4y = 8

0 + 4y = 8

       4y = 8
         y = 8/4
        y = 2
Maka titik potong di y (0, 2)

jika y = 0, maka:

2x + 4y = 8

2x + 0 = 8

        2x = 8
          x = 8/2
          x =4
Maka titik potong di x (4, 0)

Jadi titik potong persamaan 2x + 4y =8 adalah (0,2) dan (4,0)

Sekarang buat garis dari kedua persamaan tersebut berdasarkan titik potong, yakni seperti gambar di bawah ini.

Berdasarkan gambar grafik sistem persamaan dari x + 2y = 2 dan 2x + 4y = 8 di atas tampak bahwa kedua garis tersebut tidak akan pernah berpotongan. Jadi, himpunan penyelesaian dari sistem persamaan x + 2y = 2 dan 2x + 4y = 8 adalah himpunan kosong { }.

Kita akan mudah mengetahui apakah suatu sistem persamaan linear dua variabel tersebut memiliki himpunan penyelesaian atau tidak yaitu dengan cara melihat koefesien dari variabel-variabel kedua persamaan. Jika koefesiaen variabel-variabel persamaan merupakan kelipatan dari persamaan yang satunya, sudah dipastikan bahwa sistem persamaan tersebut tidak memiliki suatu penyelesaian atau penyelesaiannya berupa himpunan kosong. Untuk contoh soal silahkan simak contoh soal 2 di atas.

Pada contoh soal 2 merupakan sistem persamaan linear dua variabel yakni:

x + 2y = 2 . . .  persamaan 1

2x + 4y = 8 . . persamaan 2

Perhatikan koefisien-koefisien pada variabel x dan y. Koefisien variabel x dan y pada persamaan 2 meruapakan kelipatan dari koefisien variabel x dan y pada persamaan 1. Contoh lain sistem persamaan linear dua variabel yang himpunan penyelesaiannya berupa himpunan kosong yakni:

a) x + y = 4 dan 2x + 2y = 6

b) x – 3y = 3 dan 2x – 6y = 6

Coba buktikanlah dengan metode grafik bahwa kedua sistem persamaan linear dua variabel tersebut himpunan penyelesaiannya berupa himpunan kosong.

“Kelemahan dari metode grafik adalah anda akan kesulitan menentukan himpunan penyelesaian kedua garis tersebut berpotongan di koordinat berupa bilangan pecahan”. Misalnya contoh soal berikut, tentukan himpunan penyelesaian sistem persamaan linear dua variabel 7x + 5y = 11 dan 21x – 10y = 3 jika x, y variabel pada himpunan bilangan real.

Jika anda mengguanakan metode grafik maka Anda akan kesulitan menentukan himpunan penyelesaiannya karena himpunan penyelesaiannya berupa bilangan pecahan. Oleh karena itu kita gunakan alternatif yang kedua untuk menyelesaikan sistem persamaan linear dua variabel tersebut yakni dengan metode eliminasi. Bagaimana metode eliminasi tersebut?
Materi metode eliminasi dapat dibaca dengan klik di sini

Materi lain dapat di lihat dengan cara klik judul di bawah ini:

MATERI SPLDV 

Tags : matematika materi materinya spldv